천만개, 일억개를 탐색해야 할 때

천만개가 넘는 리스트에서 특정 값을 찾아야 할 때, 각자가 구현하는 코드는 다양할 것인데, 효율적인 탐색 방법 중 하나가 바로 이진탐색이다. 말로만 들으면 어려울 것 같지만 업-다운 게임을 생각하면 쉽다.

1~60개의 정수 중 하나 40을 맞추려고 할 때

  • 30? Up!
  • 45? Down!
  • 38(37.5를 반올림)? Up!
  • 42(41.5를 반올림)? Down!
  • 40? Yes!

이렇게 절반으로 쪼개가며 큰 지, 작은 지를 판단하고 또 절반으로 나누고를 반복하다가 찾는 수가 나올 때 탐색을 종료하는 것이 이진탐색이다. 중요한 것은 리스트들은 정렬된 상태여야 한다는 것이다. 큰 지, 작은 지를 판단하는데 리스트가 뒤죽박죽이라면 아무런 의미가 없다.

구현하는 방법

이진탐색을 구현하는 방법은 일반적으로 2가지인데, 재귀 함수로 작성하는 방법과 반복문으로 작성하는 방법이 있다. 하지만 파이썬에서는 재귀함수의 최대 재귀 횟수가 정해져 있으므로 반복문을 이용한 이진탐색을 선호하는 편이다. (물론 최대 재귀 횟수를 조정할 수 있다)

재귀를 이용한 방법

1
2
3
4
5
6
def bisearch(array,target,start,end):
    if start>end: return None
    mid = (start+end)//2
    if array[mid]==target: return mid
    elif array[mid]>target: return bisearch(array,target,start,mid-1)
    else: return bisearch(array,target,mid+1,end)

사실상 위에서 말한 업다운의 예시를 그대로 코드에 옮긴 것과 같다. start와 end를 더한 절반인 mid를 기준으로 큰 지, 작은 지, 일치하는 지를 판단하여 다시 기준을 잡고 함수를 재귀한다.

반복문을 이용한 방법

1
2
3
4
5
6
7
def bisearch(array,target,start,end):
    while start<=end:
        mid=(start+end)//2
        if array[mid]==target: return mid
        elif array[mid]>target: end=mid-1
        else: start=mid+1
    return None

while문을 사용하여 이진탐색을 하는 방법인데, 로직은 당연히 재귀함수를 사용할 때와 같다.

이제 구현한 이진탐색 코드로 숫자를 탐색해보자.

1
2
3
4
n, target = list(map(int,input().split()))
array = list(map(int, input().split()))
result = bisearch(array,target,0,n-1)
print(result if result else '원소가 존재하지 않음')

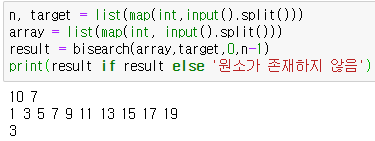
이렇게 작성한 코드는 주어진 리스트 원소의 수 n, 찾는 대상 target, 정렬된 리스트 array로 이진 탐색을 시행한 후 대상이 있을 때만 결과를 반환한다.

예시에서는 숫자의 개수가 10개이기 때문에 그냥 for loop를 돌면서 순차 탐색을 하는 것이 때로는 빠를 수도 있다. 그러나 1부터 10000000까지의 숫자 리스트에서 9999999라는 숫자를 찾는다면 효율은 비교할 수 없이 이진탐색이 빠르다.

순차탐색의 시간복잡도는 O(N)이고, 이진탐색의 시간복잡도는 O(logN)이다.

파이썬에서는 bisect가 있다

특정 라이브러리를 사용하지 말라는 조건이 없다면 파이썬에는 bisect라는 라이브러리가 있다.

1
2
3
import bisect
arr = [1,3,4,5]
print(bisect.bisect(arr, 2)) # 결과: 1

여기서 bisect() 메소드는 bisect_right()와 같은데, 2라는 숫자를 넣을 때 인덱스가 몇이어야 하는지 반환한다. 이 방법을 이용하면 어느 자리에 넣을지, 이 숫자가 어디에 있는 지도 찾을 수 있다.

bisect 라이브러리에 대한 자세한 설명은 KIM TAEWOO님의 블로그에 잘 설명되어 있다.

라이브러리를 쓰는 것은 얼마든지 좋지만 적어도 어떻게 돌아가는 지는 알고 써야한다고 생각한다.